Plot Levelset Example#

Imports#

import numpy as np

from cristal import DyCF, DyCFPlotter, IMPLEMENTED_REGULARIZATION_OPTIONS
from cristal.utils.data import make_T_rotated

Parameters#

d = 2  # Data dimension
n = 8  # Degree of the polynomial basis
N = 1000  # Number of samples

Data#

data = make_T_rotated(N)

Without regularization for DyCF#

Show the Christoffel function level sets

Fit the Christoffel function#

dycf = DyCF(n, IMPLEMENTED_REGULARIZATION_OPTIONS.CONSTANT)
dycf.fit(data)

<cristal.christoffel.DyCF at 0x7ffaf8405be0>

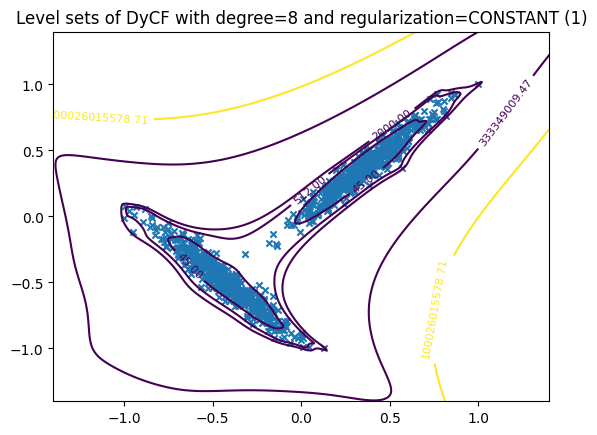
Plot the level set#

plotter = DyCFPlotter(dycf)

plotter.levelset(data, n_x1=500, n_x2=500, levels=[45, 512, 2000], percentiles=[50, 75])
# n_x1 and n_x2 control the resolution of the grid for plotting
# You can adjust the levels and percentiles as needed
# More information can be found in the odds_optimized.plotter.LevelsetPlotter.plot documentation
../../_images/ad99ed831e3d64a4f47ed7ad56ad04a626ab5f4100cd003319f5eabd0b9988d8.png

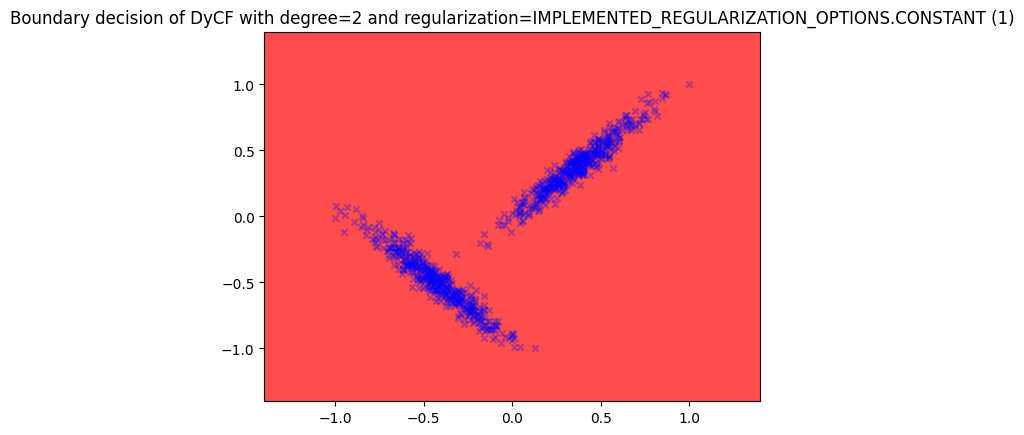
Plot the boundary decision#

Only outliers because the regularization is not set.

plotter.boundary(data, n_x1=500, n_x2=500)
../../_images/0b0a2ae677001188743408c81d17f5beb8a4d442560a14af6377338c4728d28d.png

Using “comb” regularization for DyCF#

“comb” regularization means that the level set of DyCF at 1 is equivalent to the level set of the Christoffel function at $\begin{pmatrix}n+d \ d\end{pmatrix}$, where d is the number of features and n is the degree of the polynomial.

Fit the Christoffel function#

dycf_comb = DyCF(n, IMPLEMENTED_REGULARIZATION_OPTIONS.COMB)
dycf_comb.fit(data)

<cristal.christoffel.DyCF at 0x7ffaa426b250>

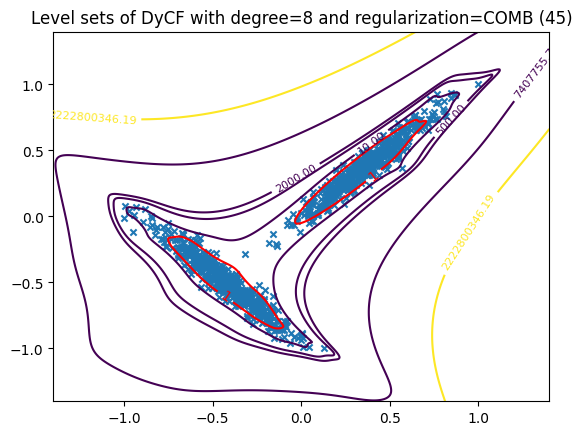
Plot the level set#

plotter_comb = DyCFPlotter(dycf_comb)

plotter_comb.levelset(data, n_x1=500, n_x2=500, levels=[10, 500, 2000], percentiles=[50, 75])
# n_x1 and n_x2 control the resolution of the grid for plotting
# You can adjust the levels and percentiles as needed
# More information can be found in the odds_optimized.plotter.LevelsetPlotter.plot documentation
../../_images/c0d1d3ef25518bba0132e61d890ba7c0d5e7f64ec0f197627ca512bcb376b8d5.png

Plot the boundary decision#

plotter_comb.boundary(data, n_x1=500, n_x2=500)
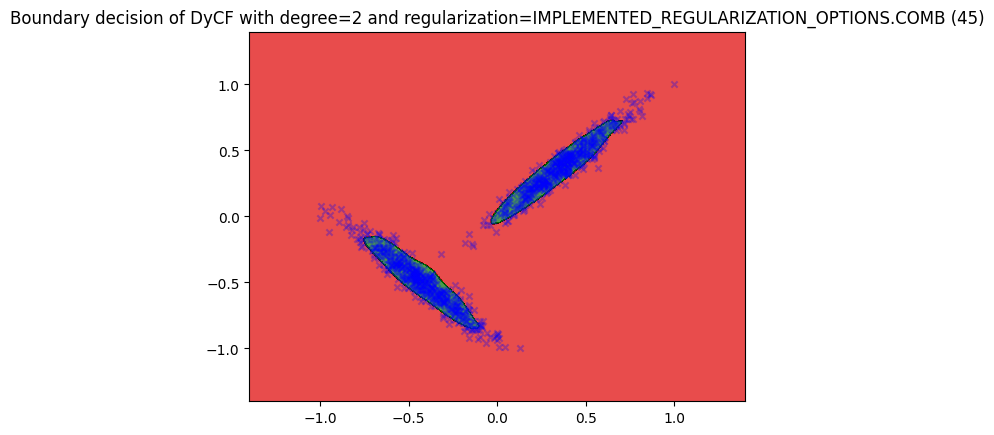
../../_images/a9c817178cb8218cddeb57a2d860ea78e22deefae257a0c52ec1c3f6e59f6360.png

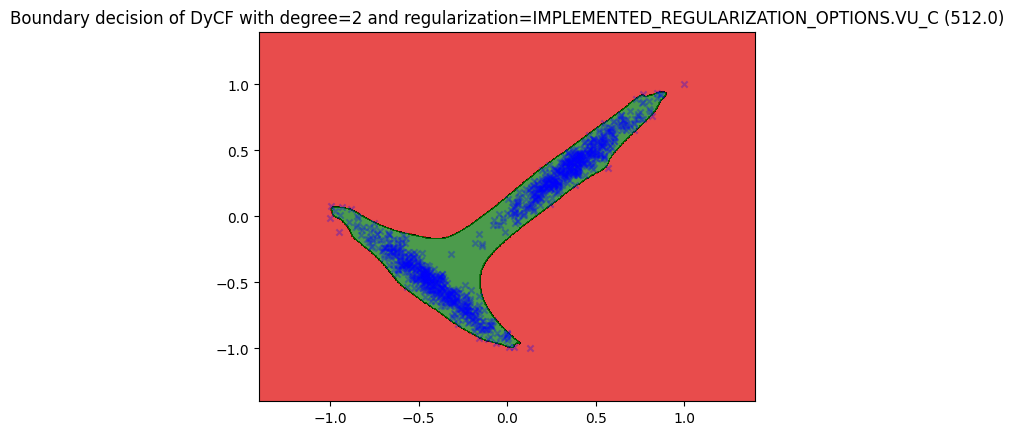
Using “vu_C” regularization for DyCF#

“vu_C” regularization means that the level set of DyCF at 1 is equivalent to the level set of the Christoffel function at $\mathbf{\frac{n^{3d/2}}{C}}$, where d is the number of features and n is the degree of the polynomial.

Fit the Christoffel function#

dycf_vu_C = DyCF(n, regularization=IMPLEMENTED_REGULARIZATION_OPTIONS.VU_C)
dycf_vu_C.fit(data)

<cristal.christoffel.DyCF at 0x7ffaa9fb47d0>

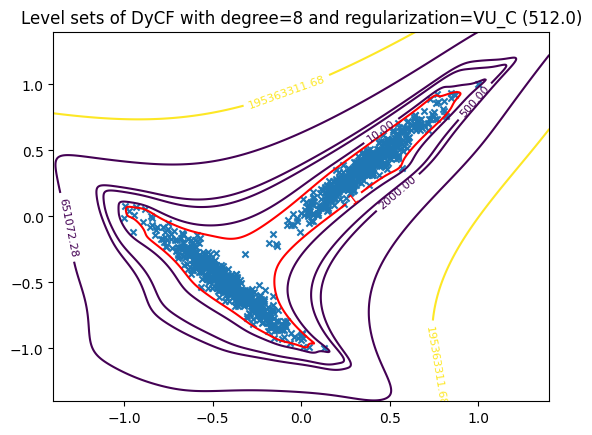
Plot the level set#

plotter_vu_C = DyCFPlotter(dycf_vu_C)

plotter_vu_C.levelset(data, n_x1=500, n_x2=500, levels=[10, 500, 2000], percentiles=[50, 75])
# n_x1 and n_x2 control the resolution of the grid for plotting
# You can adjust the levels and percentiles as needed
# More information can be found in the odds_optimized.plotter.LevelsetPlotter.plot documentation
../../_images/06378f391779b43dbe8baa66d78ff6807ca85c87adf795dd5bfd9362985c3d70.png

Plot the boundary decision#

plotter_vu_C.boundary(data, n_x1=500, n_x2=500)
../../_images/172e130d2d083ee8088ae6c3e82330dfbebac0ff68399141cb8f88fae1730a33.png